| Hier gibt's in unregelmäßiger Reihenfolge kurze spannende interessante oder ungewöhnliche Mathematik-Beiträge. |
| |
|
|
| |
|
| Restklassen modulo 6 (9. 8. 2018) |
| |
|
| Im ersten Jahr der Volksschule rechnet man nur mit natürlichen Zahlen {0, 1, 2, 3 … } - meistens im Zahlenraum bis 20. Aber danach wird's schwieriger, obwohl nach wie vor nur natürliche Zahlen verwendet werden. |
| Schade, dass man nicht einen Zahlenraum - z.B. die natürlichen Zahlen {0, 1, 2, 3, 4, 5} - vorgeben kann und nur in diesem Bereich rechnet. |
| Aber Halt! - Man kann das doch!!! |
| Ich betrachte ganzzahlige Divisionen von natürlichen Zahlen, z.B. die Division durch 6. Mich interessiert aber nicht das Ergebnis der Division, sondern der Rest. |
Bsp.: 57 : 6 = 9, Rest 3 |
| In Worten: 57 ergibt bei Division durch 6 den Rest 3. |
| In der mathematischen Sprechweise: "57 modulo 6 = 3" |
| oder |
| "57 liegt in der Restklasse 3 modulo 6" |
| Bei der Division durch 6 können nur die Reste 0, 1, 2, 3, 4 oder 5 vorkommen. Alle natürlichen Zahlen, die bei Division durch 6 z.B. den Rest 3 liefern, gebe ich in die Restklasse 3 - [3] geschrieben. |
| Somit ist jede natürliche Zahl in einer der Restklassen [0], [1], [2], [3], [4], [5] enthalten - und mehr Restklassen gibt es nicht, da bei Division durch 6 höchstens 5 als Rest vorkommen kann. |
| Die Restklasse [3] enthält die Zahlen {3, 9, 15, 21, 27, … }, die Restklasse [4] die Zahlen {4, 10, 16, 22, 28, … } |
| Wie rechnet man nun mit Restklassen? [3] + [4] = ? |
| Nehme eine beliebige Zahl aus [3] und addiere sie zu einer beliebigen Zahl aus [4], und sieh nach in welcher Restklasse sich das Ergebnis befindet: |
| 9 + 10 = 19 oder 3 + 28 = 31 oder 15 + 22 = 37 oder ….. |
| Jedes Ergebnis gibt bei Division durch den Rest 1, liegt also in der Restklasse [1]. Man kann leicht beweisen dass das mit jedem Zahlenpaar funktioniert. |
| Ebenso funktioniert die Multiplikation. |
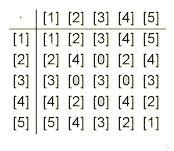
| Da ich nur mit einer beschränkten Anzahl von "Zahlen" (= Restklassen) rechne, kann ich alle Möglichkeiten in einer Tabelle aufschreiben - vorerst die Addition und die Multiplikation (auf die Multiplikation mit [0] kann man in der Tabelle verzichten, da dort immer [0] stehen würde). |

|
|
| Bem.: |
| (1) Die Rechnung [3] + [4] = [1] habe ich gelb gekennzeichnet. |
| (2) Sieht man in den entsprechenden Tabellen nach, so erkennt man, dass [5] + [4] = [3] und [3] . [2] = [0] ist. |
| (3) Wenn man auch negative ganze Zahlen zulässt, kann man auch Subtraktionen problemlos durchführen. |
| (4) Die Divisionstabelle ist etwas schwieriger. Auf Wunsch werde ich die auch angeben. |
|
| |
|
| Woher kommt das weiße Quadrat? (10. 4. 2018) |
| |
|
|
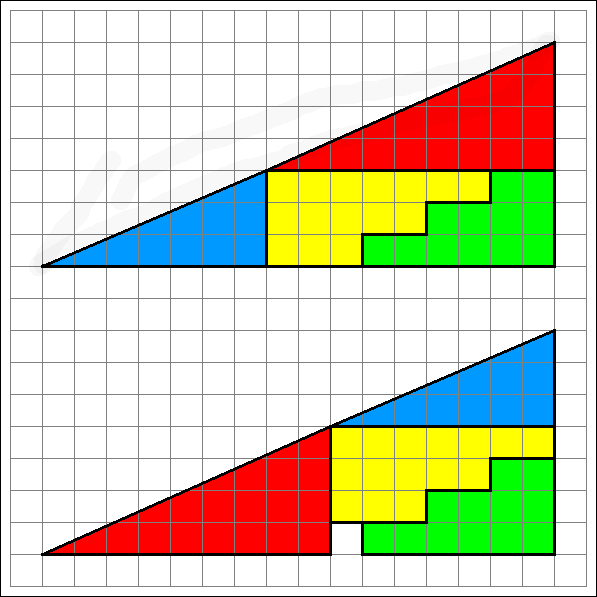
Wenn man das obere Dreieck in die bunten Teilfiguren zerschneidet - und sie dann wie in der unteren Abbildung wieder zusammenlegt, entsteht plötzlich ein weißes Quadrat mehr. Woher kommt das? |
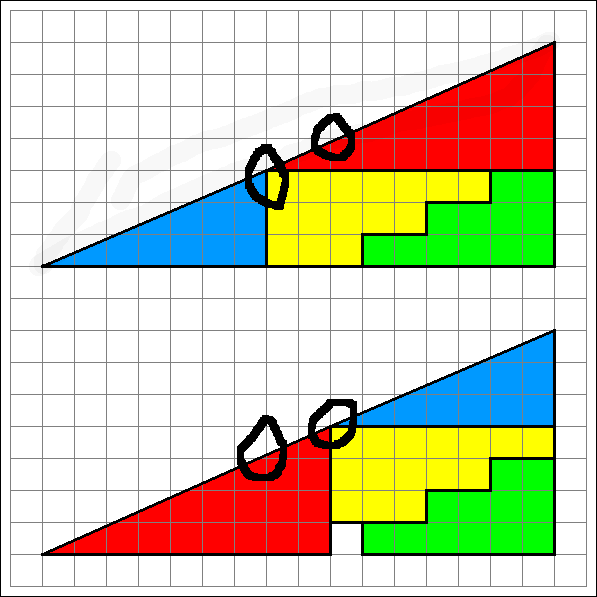
Entscheidend ist folgende Erkenntnis: das obere und das untere "Dreieck" sind nicht gleich. Genaugenommen sind beide Figuren keine extakten Dreiecke, wie die folgenden Überlegungen zeigen!Betrachte die beiden Hypotenusen (Hypotenuse = die dem rechten Winkel gegenüber liegende Seite des Dreiecks = längste Seite im rechtwikligen Dreieck): das sind keine exakten geraden Linien - die obere Hypotemuse knickt nach innen, die untere nach außen (ich habe zwei Stellen wo man das sieht eingekreist). |
|
| Mathematisch exakter:Ich betrachte, wie steil die Hypotenusen des roten und des blauen Dreiecks ansteigen. Den Anstieg definiert man als Quotient Gegenkathete / Ankathete. |
| Der Anstieg des blauen Dreiecks: 3/7 = 0,425714... , was einem Steigungswinkel von 23,2° entspricht. |
| Der Anstieg des roten Dreiecks: 4/9 = 0,444444... , was einem Steigungswinkel von fast 24° entspricht. |
| Im oberen Dreieck ist die "Hypotenuse" zuerst flacher, steigt dann steiler an - im unteren Dreieck umgekehrt. Die obere Hypotenuse hat ein kaum sichtbaren Knick nach innen, die untere einen Kick nach außen. |
| Damit ist die Fläche des unteren Dreiecks ein wenig größer - genau um das kleine weiße Quadrat. |
| |
|
|
| Das magische Quadrat von Albrecht Dürer(30. 3. 2018) |
| |
|
Ein magisches Quadrat ist eine quadratische Anordnung von natürlichen Zahlen - beginnend mit 1, sodass die Summe der Zahlen aller Zeilen, Spalten und der beiden Diagonalen gleich ist. Diese Summe wird als die magische Zahl des magischen Quadrates bezeichnet. |

|

|
Dieses magische Quadrat stammt von Abrecht Dürer und kommt in seinem Bild "Melencholia 1" vor (rechts oben im Hintergrund). |
| Dieses Quadrat bietet allerdings noch mehr: |

|
| Auch die 4 Teilquadrate, das Quadrat in der Mitte sowie die 4 Zahlen in den Ecken ergeben als Summe die magische Zahl 34. Außerdem steht in der Mitte der 4. Zeile das Entstehungsjahr 1514. |
| |
|
|
| |
|
| |
|
| Ein seltsames Problem der ebenen Geometrie (23. 2. 2018) |
| |
|
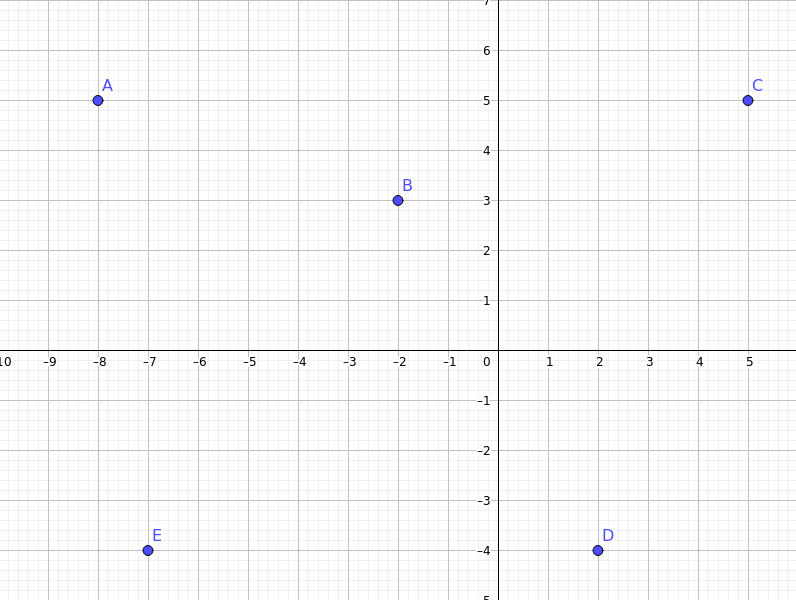
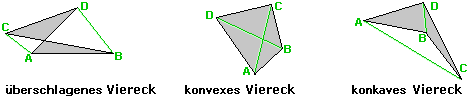
| Gegeben seien fünf beliebige Punkte in einer Ebene, wovon keine drei auf einer Geraden liegen. Dann gilt: vier dieser Punkte bilden immer ein konvexes Viereck. |
|
| Bemerkung: Ein Viereck ist konvex, wenn die beide Diagonalen innerhalb der Vierecksfläche liegen. |
|
| Der ungarischen Mathematikerin Esther Szekeres gelang in jungen Jahren als Esther Klein ein wahrhaft genialer Beweis, indem sie es erkannte, dass es eigentlich nur 3 Kombinationsmöglichkeiten der 5 Punkte gab. |

|
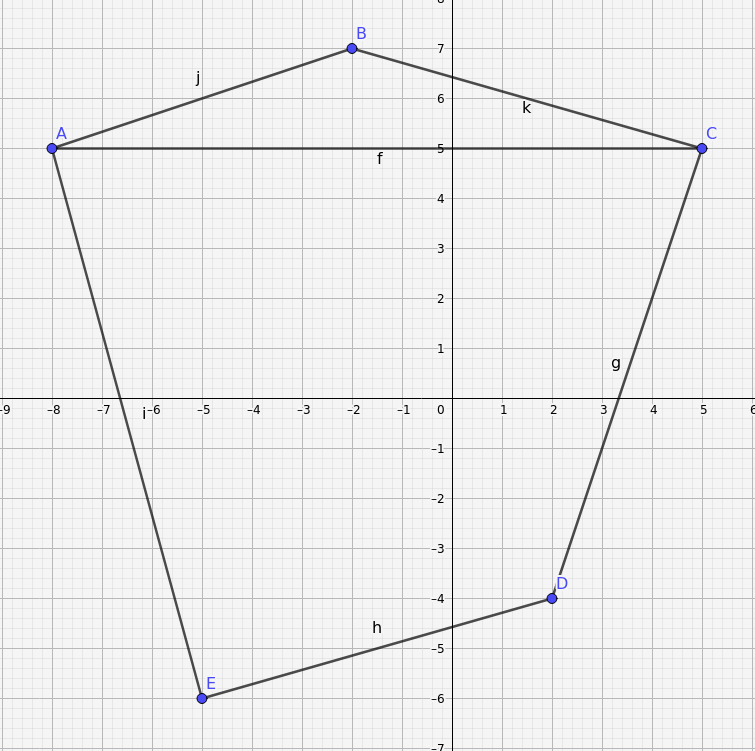
| Im ersten Fall bilden die 5 Punkte selbst ein konvexes Fünfeck; beliebige 4 der 5 Punkte bilden daher ein konvexes Viereck. |
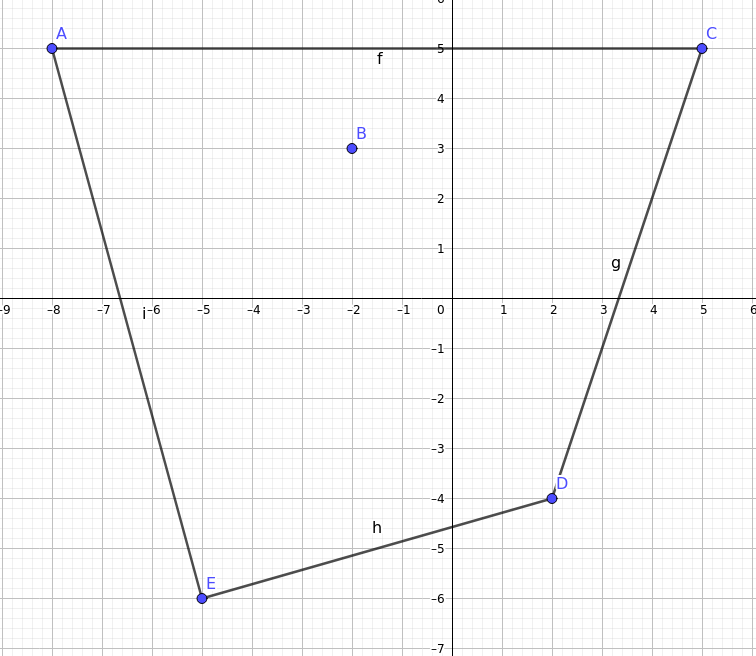
Im zweiten liegt einer der fünf Punkte innerhalb der übrigen vier; in diesem Fall bilden die vier äußeren Punkte ein konvexes Viereck. |
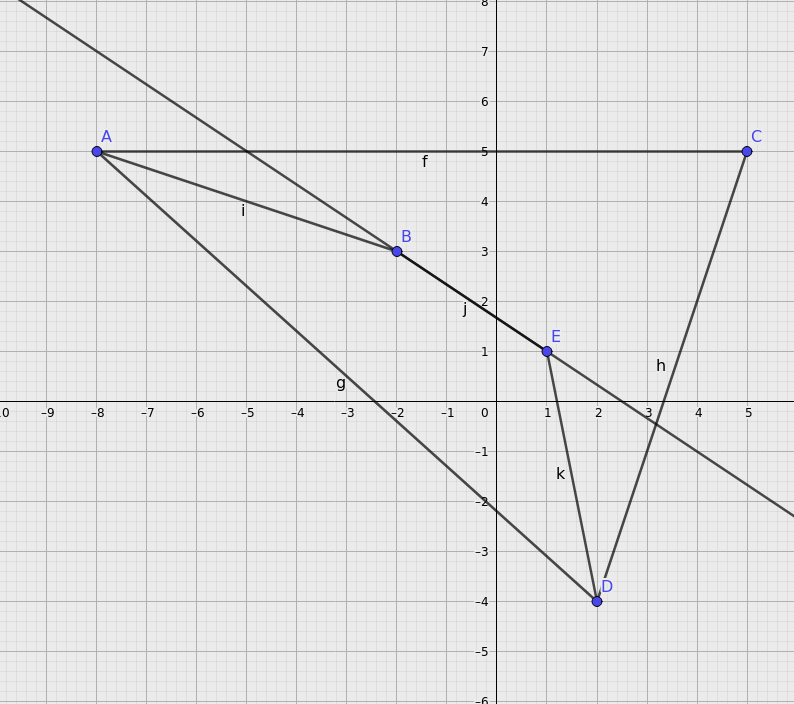
Beim dritten Fall bilden drei der fünf Punkte ein Dreieck, die anderen beiden liegen innerhalb des Dreiecks. Zieht man eine Gerade durch diese beiden inliegenden Punkte, liegen immer zwei Punkte auf der einen oder auf der anderen Seite der Geraden. Diese zwei Punkte bilden mit den beiden inliegenden Punkten immer ein konvexes Viereck. |
|
|
|
|
| |
|
| |
|
|
| |
|
| Die (3n+1) -Vermutung (20. 2. 2018) |
| |
|
| Der deutsche Mathematiker Lothar Collatz formulierte 1937 erstmal folgende Vermutung, die auch das Collatz-Problem genannt wird: |
| Nimm eine natürliche Zahl n < 0. |
| Wenn n gerade ist, bilde n : 2. |
| Ist n ungerade, so bilde 3 . n + 1. |
| Wiederhole diese Vorgangsweise mit der erhaltenen Zahl. |
| Beispiele: |
| n = 13. Dann entsteht die nachstehende Zahlenfolge:13, 40, 20, 10, 5, 16, 8, 4, 2, 1 |
| n = 27. Dann entsteht die nachstehende Zahlenfolge: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700. 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 338, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ( ... ich hoffe ich habe mich nicht verrechnet!) |
| LOthar Collatz behauptete nun, bei jeder beliebigen Startzahl führt die Folge immer zu 1. |
tr>
Diese Vermutung wurde bist heute nicht bewiesen - oder auch nicht durch ein Gegenbeispiel widerlegt. |
tr>
Wer also berühmt werden will, kann sich ja daran versuchen. 2011 meldete der Spiegel Online, dass ein Hambuger Mathematiker die Lösung gefunden hat - was sich jedoch als Irrtum herausstellte. |
| |
|
|
| |
|
| Das Königsberger Brückenproblem (17. 2. 2018) |
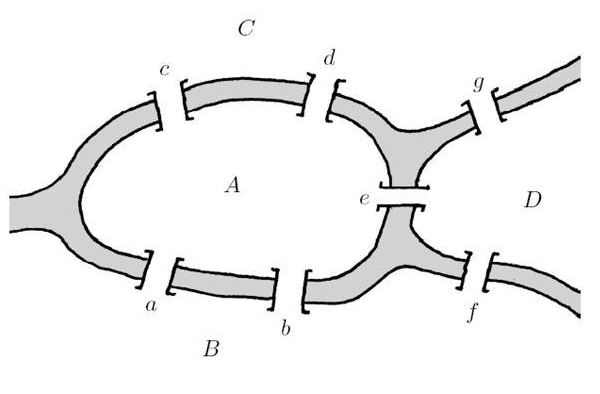
| Zur Zeit von Leonard Euler floss in Königsberg der Fluss Pregel - wie in der Abbildung rechts dargestellt. Es führten zur Insel A und zu den Stadtteilen B, C und D genau sieben Brücken. Euler stellte sich die folgende Frage: Ist es möglich, alle Brücken nacheinander zu passieren, ohne eine auszulassen oder mehr als einmal zu überschreiten? |
|
| Man könnte natürlich Zettel und Bleistift zur Hand nehmen und einfach versuchen, durch Probieren eine Lösung zu finden. Aber wann hat man alle Möglichkeiten durchprobiert? Kann man beim Probieren irgend ein System verwenden oder eine Reihenfolge angeben? Jedenfalls wird irgendwann die Vermutung auftauchen, dass es vielleicht gar keine Lösung gibt. |
| Wie kann man einen möglichen Lösungsweg beschreiben? - Indem man die Abürzungen A, B, C und D der Stadtteile aneinander reiht und so einen Weg beschreibt. BCD bedeutet z.B. vom Gebiet B in das Gebiet C und dort weiter nach D - welche Brücken dabei verwendet werden ist egal. |
| Jeder Zwischenraum zw. 2 Buchstaben entspricht dabei einer Brücke. Da ich 7 Brücken habe, benötige ich für die Beschreibung des Wegs 8 Buchstaben - wobei natürlich A, B C und D auch mehrfach vorkommen. |
| Als Nächstes überlege ich, wie oft jeder Buchstabe in dieser Buchstabenkette vorkommen muss. In das Gebiet B führen 3 Brücken:entweder beginne ich mit B und benutze eine Brücke, dann kommt B nochmals vor, wenn ich über die 2. Brücke B betrete und über die dritte verlasse. B muss als 2x aufscheinen. Ebenso verhält es sich, wenn ich in B ende. Die gleichen Überlegungen gelten für die Gebiete C und D. |
| Ähnlich verfahre ich bei der Insel A: entweder Start auf A, dann zweimaliger Durchmarsch, oder in A endet der Weg. Auf jeden Fall brauche ich A 3x in der Kette. |
A 3x, B 2x, C 2x und D 2x - das sind 9 Buchstaben (unanbhändig von der Reihenfolge). 8 Buchstaben anordnen und 9 Buchstaben verwenden geht nun wirklich nicht. |
Die logische Folgerung: es lässt sich kein Weg finden, der über jede Brücke genau einmal führt - die Aufgabe ist daher nicht lösbar. |
Diese Aufgabe gehört zum mathematischen Teilgebiet der Topologie. Erwähnenswert ist in diesem Zusammenhang, dass man in der Mathematik auch beweisen kann, dass es etwas nicht gibt. |
| |
|
| |
|
| |
|













